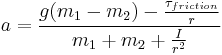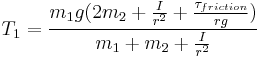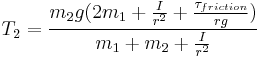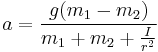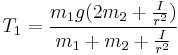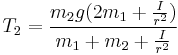Atwood machine

The Atwood machine (or Atwood's machine) was invented in 1784 by Rev. George Atwood as a laboratory experiment to verify the mechanical laws of motion with constant acceleration. Atwood's machine is a common classroom demonstration used to illustrate principles of classical mechanics.

The ideal Atwood Machine consists of two objects of mass m₁ and m₂, connected by an inextensible massless string over an ideal massless pulley. ^[1]

When m₁ = m₂, the machine is in neutral equilibrium regardless of the position of the weights.

When m₁ ≠ m₂ both masses experience uniform acceleration.

1 Equation for constant acceleration
2 Equation for tension
3 Equations for a pulley with inertia and friction
- 3.1 Practical implementations
4 See also
5 Notes

Equation for constant acceleration

We are able to derive an equation for the acceleration by using force analysis. If we consider a massless, inextensible string and an ideal massless pulley, the only forces we have to consider are: tension force (T), and the weight of the two masses (W₁ and W₂). To find an acceleration we need to consider the forces affecting each individual mass. Using Newton's second law (with a sign convention of 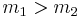$m_1>m_2$ ) we can derive a system of equations for the acceleration (a).

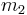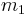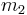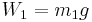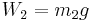As a sign convention, we assume that a is positive when downward for $m_1$ , and that a is positive when upward for $m_2$ . Weight of $m_1$ and $m_2$ is simply $W_1 = m_1 g$ and $W_2 = m_2 g$ respectively.

Forces affecting m₁:

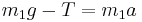
$\; m_1g-T=m_1a$

Forces affecting m₂:

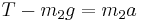
$\; T-m_2g=m_2a$

and adding the two previous equations we obtain

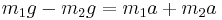$\; m_1g-m_2g=m_1a%2Bm_2a$ ,

and our concluding formula for acceleration

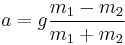
$a = g{m_1-m_2 \over m_1%2Bm_2}$

Conversely, the acceleration due to gravity, g, can be found by timing the movement of the weights, and calculating a value for the uniform acceleration a: 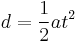$d = {1 \over 2} at^2$ .

The Atwood machine is sometimes used to illustrate the Lagrangian method of deriving equations of motion. ^[2]

Equation for tension

It can be useful to know an equation for the tension in the string. To evaluate tension we substitute the equation for acceleration in either of the 2 force equations.

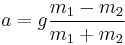
$a = g{m_1-m_2 \over m_1 %2B m_2}$

For example substituting into 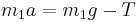$m_1 a = m_1 g-T$ , we get

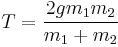
$T={2 g m_1 m_2 \over m_1 %2B m_2}$

The tension can be found in using this method.

Equations for a pulley with inertia and friction

For very small mass differences between m₁ and m₂, the rotational inertia I of the pulley of radius r cannot be neglected. The angular acceleration of the pulley is given by the no-slip condition:

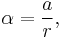
$\alpha = {a\over r},$

where $\alpha$ is the angular acceleration. The net torque is then:

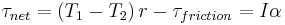
$\tau_{net}=\left(T_1 - T_2 \right)r - \tau_{friction} = I \alpha$

Combining with Newton's second law for the hanging masses, and solving for T₁, T₂, and a, we get:

Acceleration:

$a = {{g (m_1 - m_2) - {\tau_{friction} \over r}} \over {m_1 %2B m_2 %2B {{I} \over {r^2}}}}$

Tension in string segment nearest m₁:

$T_1 = {{m_1 g (2 m_2 %2B {{I} \over {r^2}} %2B {{\tau_{friction}} \over {r g}})} \over {m_1 %2B m_2 %2B {{I} \over {r^2}}}}$

Tension in string segment nearest m₂:

$T_2 = {{m_2 g (2 m_1 %2B {{I} \over {r^2}} %2B {{\tau_{friction}} \over {r g}})} \over {m_1 %2B m_2 %2B {{I} \over {r^2}}}}$

Should bearing friction be negligible (but not the inertia of the pulley and not the traction of the string on the pulley rim), these equations simplify as the following results:

Acceleration:

$a = {{g (m_1 - m_2)} \over {m_1 %2B m_2 %2B {{I} \over {r^2}}}}$

Tension in string segment nearest m₁:

$T_1 = {{m_1 g (2 m_2 %2B {{I} \over {r^2}})} \over {m_1 %2B m_2 %2B {{I} \over {r^2}}}}$

Tension in string segment nearest m₂:

$T_2 = {{m_2 g (2 m_1 %2B {{I} \over {r^2}})} \over {m_1 %2B m_2 %2B {{I} \over {r^2}}}}$

Practical implementations

Atwood's original illustrations show the main pulley's axle resting on the rims of another four wheels, to minimise friction forces from the bearings. Many historical implementations of the machine follow this design.

An elevator with a counterbalance approximates an ideal Atwood machine and thereby relieves the driving motor from the load of holding the elevator cab — it has to overcome only weight difference and inertia of the two masses. The same principle is used for funicular railways with two connected railway cars on inclined tracks.

Notes

^ Tipler, Paul A. (1991). Physics For Scientists and Engineers, Third Edition, Extended Version. New York: Worth Publishers. ISBN 0-87901-432-6. Chapter 6, example 6-13, page 160.
^ Goldstein, Herbert (1980). Classical Mechanics, second Edition. New Delhi: Addison-Wesley/Narosa Indian Student Edition. ISBN 81-85015-53-8. Section 1-6, example 2, pages 26-27.

"Atwood's Machine" by Enrique Zeleny, The Wolfram Demonstrations Project.